I don’t usually play CTFs, but this time i wanted to improve my radare2 and reversing skills.
All crackme challanges can be found here.
Levels from 1 to 3 are really entry-level, from 4 ahead start to be interesting.

As the README says: “It’s reverse engineering, not cracking.”. That means we don’t have to patch the binary in order to get the “flag”. Instead, we have to reverse engineer it, understand the algorithm, reproduce it and get the right password.

First look

First of all, let’s take a look at what it does just by executing it:

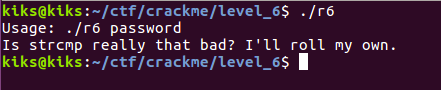
It’s telling us the usage, so following it we reach a ‘Password KO’:

Ok, our aim is to guess the password, so let’s open it in radare2 and let’s see what we can get.
Running the command iz, we can inspect for some useful strings:

We don’t see anything really useful from strings, maybe the string “this_might_be_related”, so let’s appoint it but go ahead, we can return to this string later.

With the afl command from radare2, we can get the functions list:

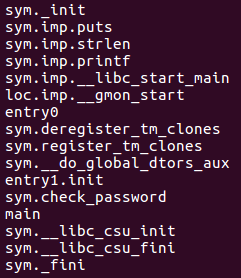
The function check_password seems interesting, but first of all let’s see what our main function do.

Main Function

After checking the correct usage of the program, the main call the check_password function and test the result of it.

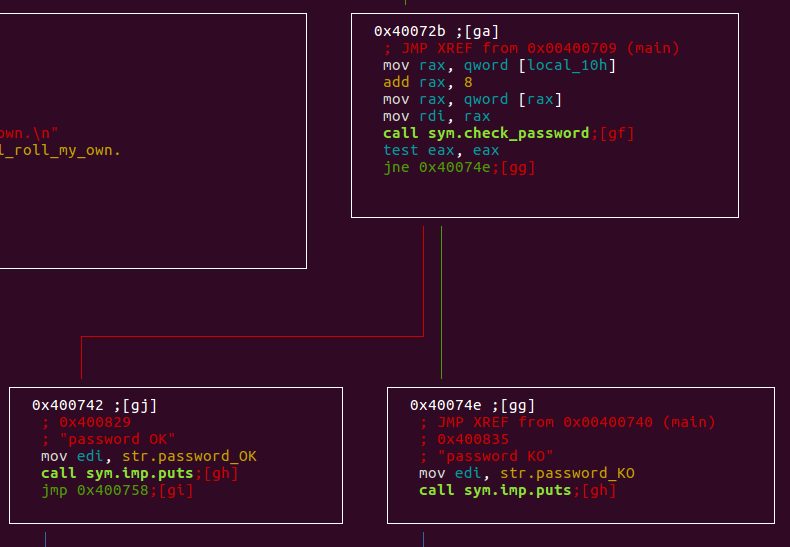
If the return value of check_password is different from zero, then it will output “Password KO”. Else, if the return value is 0, it will output “Password OK”.

Our aim is to return 0 from check_password, in order to print “Password OK”

Check Password

Password Length

The check_password function checks if the password length is 0x15 (21 in decimal): if the length is different, than it will return -1 to main, resulting in the bad password case.

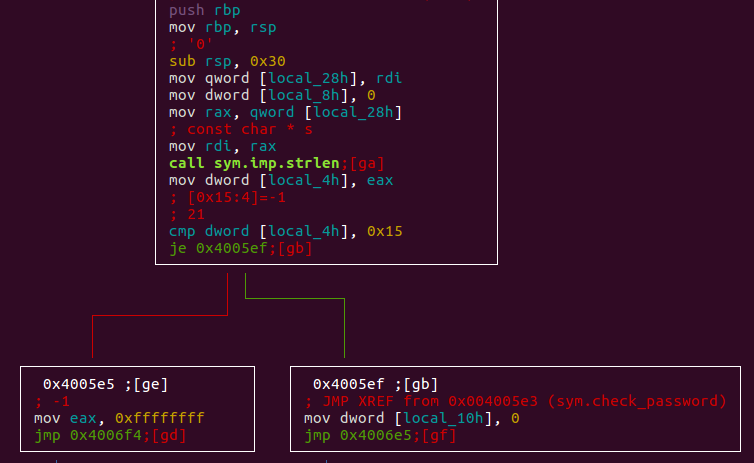
If the password length is 0x15, the decryption routine can start.

We can also see some variable initialization that can be useful in further analysis.

local_28h → input_pwd – Input password
local_4h → len_input – Input password length

We rename these variables to have meaningful names. This will help us later.

Also we have 2 zero initializations, that we have to take note:

local_8h
local_10h

So, we can add a condition to get the password:

Password must be 0x15 (21) of length

Returning Phase

First to deal with the decryption phase, we want to understand what we are returning back.

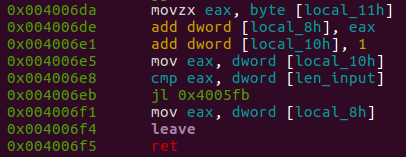
The return value is local_8h, that is the result of the addition with itself and local_11h.

Variables:

Local_8h → return_result – The return value of the function
Local_11h → sum_return_result – A value that is continually added to the return value
Local_10h → global_index – An index (deduced from the incrementing at the end of the loop)

The condition will jump back (to the loop) if the value of local_10h (the index) is lower than the length of the input password (that must be 0x15).

That’s mean that we are executing this loop 0x15 (21) times.

From these few lines of assembly we can try to produce a more explanation pseudocode:

Pseudocode 1.0	Pseudocode 2.0
eax = local_11hlocal_8h = local_8h + eaxlocal_10h = local_10h+1eax = local_10hif (eax < local_4h)repeatelseeax = local_8hret	return_result += sum_return_resultglobal_index += 1if (global_index < len_input)repeatelsereturn return_result

If we want to return 0 from the check_password function, return_result must be 0, so also sum_return_result must be 0 at each cycle of the loop.

Decryption Phase

Now we have to deal with the central part of the routine, the decryption.

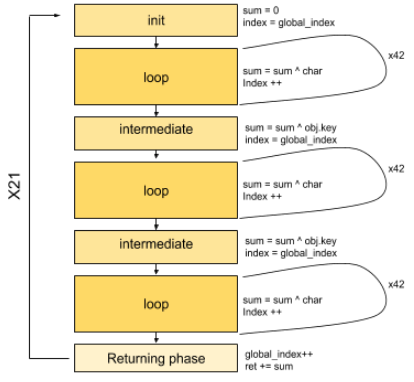
First of all, this phase is executed 21 times (we know this from the returning stage step described above) and contain:

An initialization block.
3 identical loops.
Intermediate blocks between the first and second one, the second one and the third one.

After the third loop we have the Returning phase (already described above).
The base concept can be illustrated as follow:

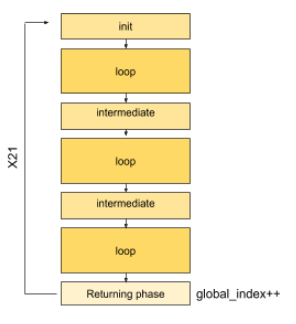
Init stage

At the init stage we are just initializing sum_return_result with 0, and copying the value of the global index into the local_ch.

Local_ch is a local index of the loop stage, so we can rename it in index

Loop stage

At this stage, we have a xor operation between each single character of the input password and sum_return_result. The xor result is placed into sum_return_result, and then recalculated with a xor between it and the next character of the input. The ‘indexing’ process is handled by an idiv instruction, that get the reminder between the index of the loop and input_len:

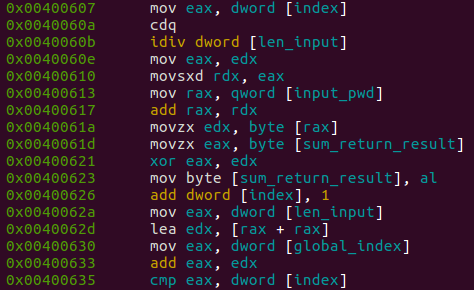
The flow of the loop stage can be drawn as:

where sum is the abbreviated version of sum_return_result.

In the case of the first loop encountered, where sum_return_result is previously initialized with 0, if we suppose that the first character is an A (0x41 hexadecimal) we have:

0x00 ^ 0x41 = 0x41 [odd]

0x41 ^ 0x41 = 0x00 [even]

0x00 ^ 0x41 = 0x41 [odd]

0x41 ^ 0x41 = 0x0 [even]

That’s mean, if we iterate for 42 times (odd), in sum_return_result we will have the character value. so the output of the first loop will always be a character of our input password.

In the following 2 loops, with sum_result_return modified by the previous one, the flow is the same described above, but the return value is no more the original character, but a xored version of it.

Intermediate stage

In the Intermediate stage, we are xoring the sum_return_result (returned from the loop stage) with a key (obj.key). The result go into sum_return_result. In the second intermediate block (after the second loop), we are doing the same but with a different key (str.this_might_be_interesting).

Then, we are moving into index (the local index used in loop stages) the value of global_index, and jump to the next loop.

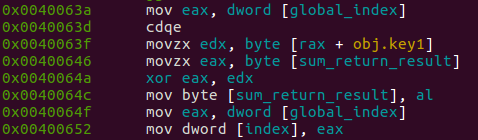
Extract keys

We need to dump both keys used in the xor operation at intermediate levels, in order to write the decryption algorithm.

We can get these keys in different methods, one way is to use the examine command from r2:

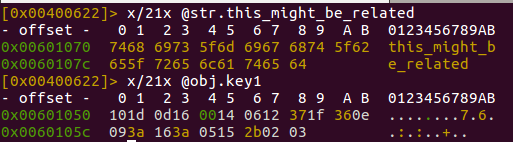
High level

Putting all together, this can be the illustrative flow (semplified):

To better play and understand the algorithm, i wrote the same algorithm at higher level (python).

The loop, in python, looks like this:

And we are integrating all like this: 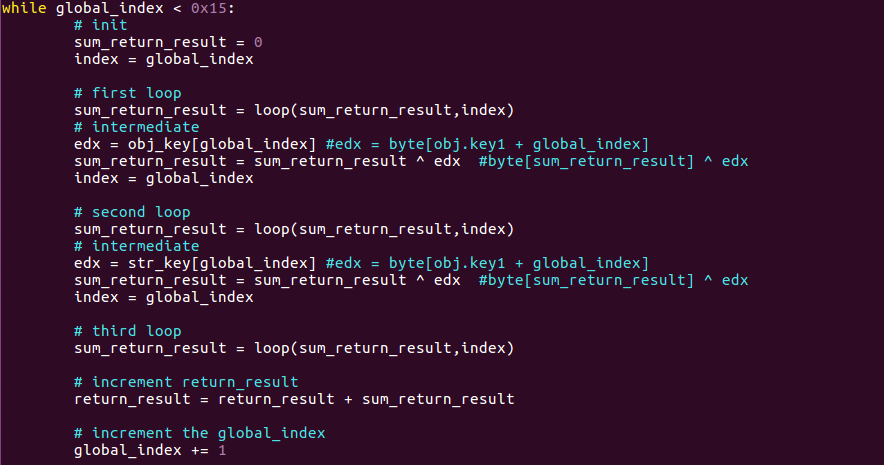undefined

I could delete the index value and use global_index instead, but i prefer to mantain the main structure of the original function

The rest of the code is similar, and included in a global loop (repeating it for 0x15 times).

With some prints at the end of each loop and intermediate blocks, we can get an output like this.

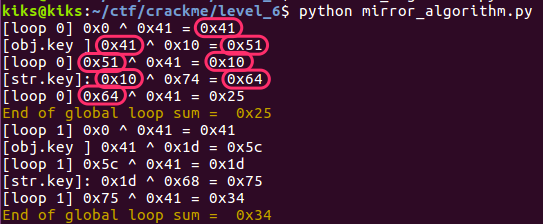
As we can see, the output of each block (a loop or intermediate) will be a xor operand for the next block.

The “End of global loop sum” will be the value added at the returned result at the end.

So, our aim is to get a 0 here.

The entire global loop can be translated with the following expression:

(((char ^ obj.key) ^ char) ^ str.key) ^ char

We need that this expression returns 0, so we can write an equation:

(((char ^ obj.key) ^ char) ^ str.key) ^ char = 0

Where, at the last XOR, the value of previously operations must be the char value, in order to return 0 :

We can split this expression in four operations:

char ^ obj.key = res1
res1 ^ char = res2
res2 ^ str.key = res3
res3 ^ char = res_final

If the final result (res_final) must be 0:

The 4th operation must contain in res3 the value of char (a xor with same values is equal to 0)
The 3rd operation must return the character value.
The 2nd operation must return a value that xored later in operation 3 will return the char value.
The 1st operation must return a value that xored in operation 2 and then 3 will return the char value at the last operation.

With this knowledge, we can write the script to generate the password.

Generate the password

Now that we know how our input is “decrypted”, we can generate it with a little script.

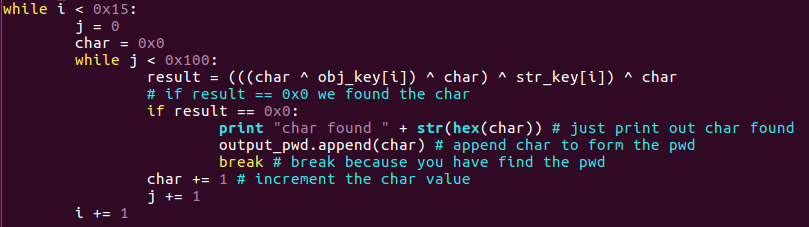
Mainly, this little script will calculate the expression with char values starting from 0x0 to 0x100 (256).

When the result of the expression is equal to 0, then it will append the character to an array that will contain the complete password, and break (skip to next character).

From the script:

Obj_key and str_key are the keys extracted before.
The first while is 0x15 because is the length of the needed password (and also the length of the key arrays)
In the second while, 0x100 is the maximum value to put into a char (is enough to find the correct value).

And the result will be:

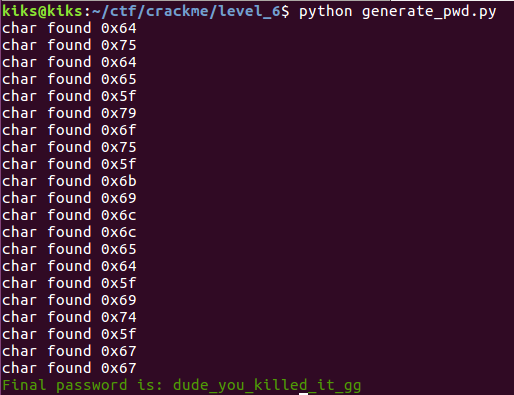
And:

Got it !

Just for fun

If we execute our previously script (the algorithm in python) with the correct password (dude_you_killed_it_gg), now the output will be:

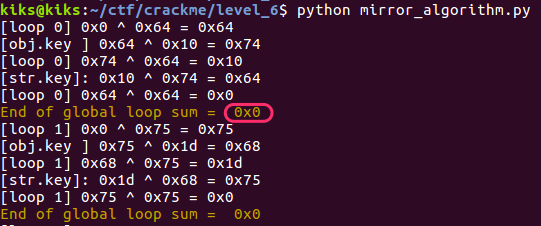
As we can see, at the fourth operation we now have the xor between the same character, resulting in 0x0. The same with the second loop and so on until the end of the global loop.